
8일 차다.
벌써 2일밖에 남지 않았다니... 뭔가 아쉬운 것 같다.
그래도 매일 오전에 알고리즘 문제를 푸는 습관은 확실히 들은 것 같다.
Day 8. 병든 나이트
오늘의 문제는 백준 프로그래밍 1783번 문제다.
문제
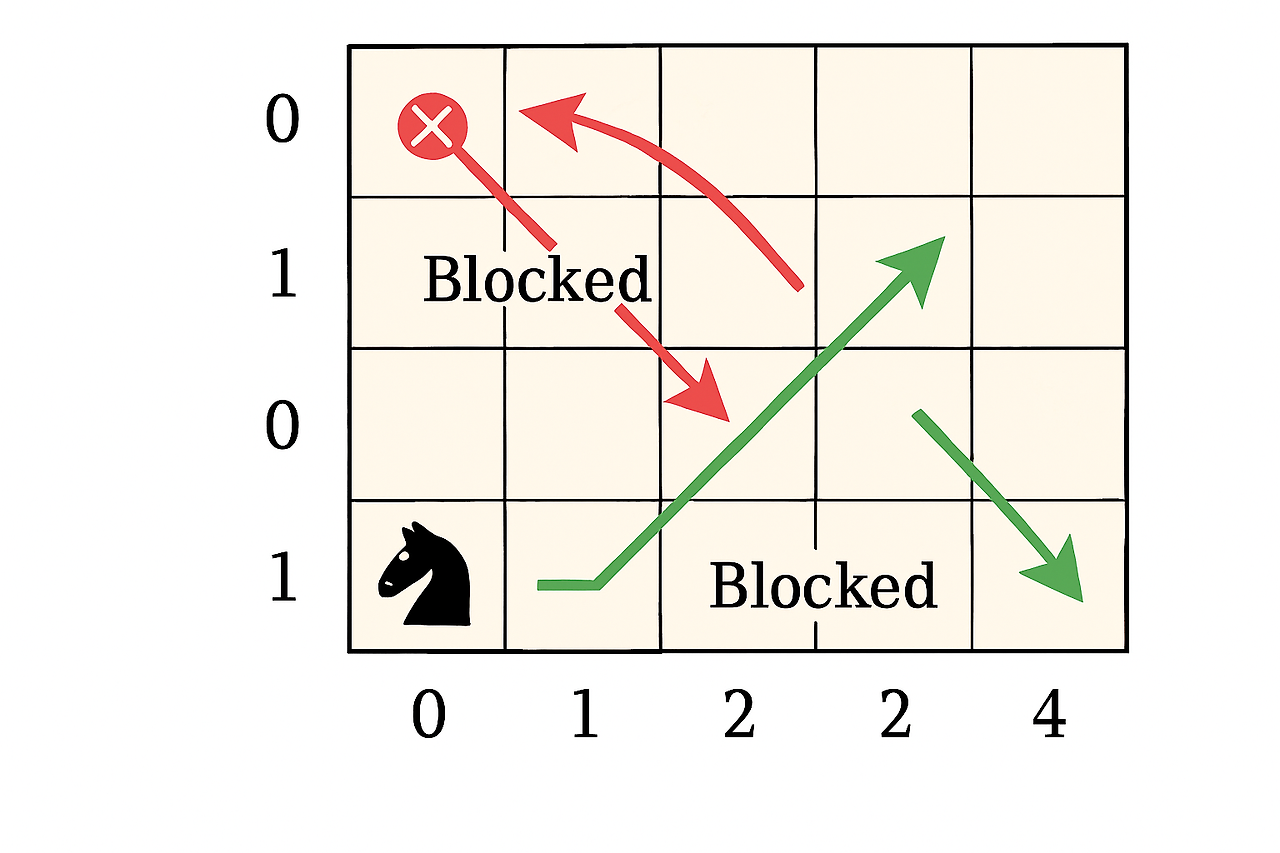
병든 나이트가 N × M 크기 체스판의 가장 왼쪽아래 칸에 위치해 있다. 병든 나이트는 건강한 보통 체스의 나이트와 다르게 4가지로만 움직일 수 있다.
- 2칸 위로, 1칸 오른쪽
- 1칸 위로, 2칸 오른쪽
- 1칸 아래로, 2칸 오른쪽
- 2칸 아래로, 1칸 오른쪽
병든 나이트는 여행을 시작하려고 하고, 여행을 하면서 방문한 칸의 수를 최대로 하려고 한다. 병든 나이트의 이동 횟수가 4번보다 적지 않다면, 이동 방법을 모두 한 번씩 사용해야 한다. 이동 횟수가 4번보다 적은 경우(방문한 칸이 5개 미만)에는 이동 방법에 대한 제약이 없다.
체스판의 크기가 주어졌을 때, 병든 나이트가 여행에서 방문할 수 있는 칸의 최대 개수를 구해보자.
입력
첫째 줄에 체스판의 세로 길이 N와 가로 길이 M이 주어진다.
N과 M은 2,000,000,000보다 작거나 같은 자연수이다.
출력
병든 나이트가 여행에서 방문할 수 있는 칸의 개수 중 최댓값을 출력한다.
예제 입출력 (표로 대체)
| 입력 | 출력 |
| 100 50 | 48 |
| 1 1 | 1 |
| 17 5 | 4 |
| 2 4 | 2 |
| 20 4 | 4 |
풀이 과정
먼저 코드 없이 알고리즘적으로 중요한 포인트들을 짚어보았다.
1. N, M을 입력받고, 판 크기에 따른 이동 패턴 가능 여부로 케이스를 분류
2. 각 케이스별로 미리 도출한 규칙에 따라 최대 이동 칸 수를 계산
경우의 수 분기 나누기
문제에서 병든 나이트가 이동할 수 있는 경우의 수는 총 네 가지다.
네 가지 이동 방법을 기반으로 다음과 같이 분기(케이스)를 분류할 수 있다.
- 세로 높이(N)가 1
- 위아래 이동 자체 불가 → 시작 칸 이외 이동 불가 → 한 가지 경우
- 세로 높이(N)가 2
- 세로 이동이 최대 1칸만 가능 → 일부 이동패턴만 가능(두 번째, 세 번째 이동 방법)
- 오른쪽으로 갈 수 있는 칸 수도 제한됨 → 두 번째 경우
- 세로 높이(N) ≥ 3, 가로 길이(M) < 7
- 세로는 충분하지만 가로가 좁아서 네 가지 이동 모두 못 씀
- 최대 4칸까지만 움직일 수 있음 → 세 번째 경우
- 세로 높이(N) ≥ 3, 가로 길이(M) ≥ 7
- 네 가지 이동 모두 가능 → 매 이동마다 오른쪽 진행 가능 → 최대 M-2 공식 → 네 번째 경우
구현
각 분기에 대해서는 이해했는데, 최대 이동 칸 수를 어떤 규칙(공식)을 기반으로 구현해야 할지 몰라서 어려움이 있었다.
우선, 네 가지 방향 이동이 가능하지만 제한된 보드판 내에서 "최대 이동 칸 수"를 이동하기 때문에 DFS/BFS 기반 탐색이 아닌, 그리디로 풀어야 한다는 점을 알 수 있었다. 즉, knight_directions 또는 visited 기반으로 한 탐색은 필요 없다.
문제는 공식을 어떻게 알 수 있는가였다.
먼저, N이 1인 경우와 N이 4인 경우에 대한 도출이 가능했다.
- 세로 높이(N)가 1
- 세로가 1줄이면 병든 나이트가 세로로 이동할 수 없으므로 움직일 수 있는 칸은 처음 위치 1칸뿐
- N이 3 이상 & M이 7 미만
- 최대 4칸까지 이동 가능
- 그리고 가로가 좁으므로 최대 $\min\left(4, 1\right)$
- 세로 높이(N) ≥ 3, 가로 길이(M) ≥ 7
- 네 가지 이동법 모두 사용할 수 있어 공간 제한이 없음
- 첫 4회 이동에서 네 가지 방법을 모두 쓴 뒤에는 계속 오른쪽으로 1칸씩 전진할 수 있음
- 최대 이동 칸 수는
하지만 N이 2인 경우에 대해서는 답을 알 수 없었다. 결국 LLM의 도움을 받았다.
N이 2인 경우, 최댓값은 다음과 같은 방식으로 도출할 수 있다.
- 오른쪽으로 이동할 때마다 2칸씩 이동
- 방문 가능한 칸들은 가로 인덱스상에서 (0, 2, 4, 6, ...) 형태로 존재
- 그만큼 최대 방문 가능한 칸 개수는 $\left\lfloor \frac{M-1}{2} \right\rfloor + 1$ 가 됨
- (M−1) // 2는는 오른쪽으로 점프할 수 있는 최대 횟수
- +1은 시작 칸 포함
- 단, 문제 제약으로 최대 4칸까지만 방문 가능
즉,
$$
\min\left(4, \left\lfloor \frac{M-1}{2} \right\rfloor + 1 \right)
$$
이 된다.
이걸 도출해 내는 방식은... 직접 그려보고, 연습해서 도달하면 된다고 한다...
개선점

완전탐색 대신 규칙을 찾고자 한 것은 좋은 접근이었지만, 아직 수학적 사고력을 기반으로 공식을 도출하는 것은 어려운 것 같다.
돌이켜보면 N = 2의 경우도 알아낼 법했지만, 너무 어렵게 생각했던 것 같다.
조건 분기 로직 구성 능력을 기를 수 있도록 노력해야겠다.
'개발자 일기 > 알고리즘 공부' 카테고리의 다른 글
| 작심큰일 챌린지 - Day 10. 김밥천국의 계단 (미들러, Python) (5) | 2025.08.15 |
|---|---|
| 작심큰일 챌린지 - Day 9. 나의 인생에는 수학과 함께 (미들러, Python) (3) | 2025.08.14 |
| 작심큰일 챌린지 - Day 7. 섬의 개수 (미들러, Python) (1) | 2025.08.12 |
| 작심큰일 챌린지 - Day 6. JadenCase 문자열 만들기 (미들러, Python) (1) | 2025.08.11 |
| 작심큰일 챌린지 - Day 5. 피보나치 비스무리한 수열 (미들러, Python) (5) | 2025.08.08 |




댓글