
4일 차가 되었다.
확실히 매일 아침마다 문제를 푸는 것이 습관 형성이 되어있지 않아 그런가... 쉽지 않다.
기존의 루틴이 조금 꼬여서 시간을 잘 쓰기 위해 나름 애쓰는 중이다.
Day 4. 너구리 구구
오늘의 문제는 백준 프로그래밍 18126번 문제다.
문제
텔레토비 동산에 사는 너구리 구구는 입구, 거실, 주방, 안방, 공부방, 운동실, 음악실, 음식 창고 등 N개의 방을 가지고 있다. 입구를 포함한 모든 방은 1부터 N까지의 번호가 있고, 입구는 1번이다. 구구의 집으로 들어가는 입구는 한 개이며 입구과 모든 방들은 총 N-1개의 길로 서로 오고 갈 수 있다.
구구는 스머프 동산에서 멜론아 아이스크림을 발견했다. 구구는 무더운 여름 햇살을 피해 최대한 입구에서 먼 방에 아이스크림을 숨기려고 한다.
구구가 집 입구에서 멜론아 아이스크림을 숨기려고 하는 방까지 이동하는 거리를 구하여라.
입력
- 첫째 줄에 정수 N(1 ≤ N ≤ 5,000)이 주어진다.
- 다음 N-1개의 줄에 구구의 집의 모든 길의 정보가 정수 A, B, C(1 ≤ A, B ≤ N, 1 ≤ C ≤ 1,000,000,000)로 주어진다.
- A번 방과 B번 방 사이를 양방향으로 연결하는 길의 길이가 C임을 의미한다.
출력
구구가 집 입구에서 멜론아 아이스크림을 숨기려고 하는 방까지 이동하는 거리를 구하여라.
예제 입력 1
4
1 2 3
2 3 2
2 4 4예제 출력 1
7
풀이 과정
그래프 vs. 트리 구조
먼저 문제의 핵심 조건을 다시 정리했다.
1. 입구(1번 노드)를 포함하여 N개의 방(노드)이 있다.
2. 모든 방과 방은 N-1개의 양방향 길(간선)로 연결되어 있다.
3. 모든 방이 하나로 연결되어 있고, 사이클(순환)이 없다.
4. 각 길에는 길이(가중치)가 있다.
한 개의 입구, 모든 방들이 서로 오고 갈 수 있는 방...
처음에는 그래프 구조인가 했는데, "N개의 노드와 N-1개의 간선으로 모두 연결되어 있다"는 말은 사이클(경로 중간에 같은 노드를 두 번 이상 방문)이 없다는 뜻이라 트리 구조 문제로 해석하는 것이 맞다.
핵심 조건은 정리했지만 입력 부분에서 "N-1개의 줄에 구구의 집의 모든 길의 정보가 정수 A, B, C로 주어진다"는 말이 정확히 무슨 의미인지 이해가 되지 않았다.
해당 입력에 대한 조건은 "두 방 사이의 직접 연결된 길(간선)과 그 길의 길이(가중치)"와 같다.
따라서, 예제 입력 1을 해석해자면 다음과 같다.
4 ← 방(노드)의 개수: 4개
1 2 3 ← 1번 방과 2번 방이 길이 3인 길(간선)로 연결
2 3 2 ← 2번 방과 3번 방이 길이 2인 길로 연결
2 4 4 ← 2번 방과 4번 방이 길이 4인 길로 연결
이를 그림으로 표현하면 다음과 같다.
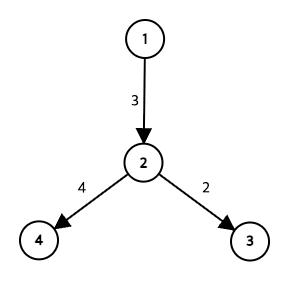
우리가 익히 알고 있는 이진 트리와는 조금 다르지만, 트리 구조임을 알 수 있다.
DFS vs. BFS
이번 문제에서 어떤 탐색 방식이 좋은지 고민해 보았지만, 쉽게 결론 내릴 수 없어 AI에게 물어보았다.
그 이유는 다음과 같다:
- 최장 경로를 구하는 문제
- BFS는 무가중치 그래프에서 최단 경로를 빠르게 찾는 데 특화되어 있지만, 가중치가 있는 그래프에서는 단순 BFS로 최단 혹은 최장 경로를 바로 구하기 어렵습니다.
- 이 문제는 각 간선에 가중치(길이)가 있으며, 입구(1번 노드)에서 가장 먼 노드까지의 최장 거리(누적 거리)를 구하는 문제로, DFS를 통해 재귀적으로 각 경로를 따라가며 누적 거리를 계산하는 방식이 직관적이고 구현이 간단합니다.
- 경로 추적과 누적 값 계산 용이
- DFS는 한 경로를 끝까지 탐색하고 누적 거리 계산 후 되돌아가 다음 경로를 탐색하기 때문에, 경로별 누적 값을 기록하거나 처리하기에 편리합니다.
- BFS는 레벨 단위로 탐색하여 최단 거리 계산에는 유용하지만, 가중치가 다를 때 가중치를 고려한 최장 경로 계산에는 추가 작업이 필요합니다(예: 다익스트라, 우선순위 큐 등이 필요).
- 트리 구조에서는 DFS가 자연스럽다
- 트리는 사이클이 없고 모든 노드가 연결된 구조이므로 DFS를 통해 루트(입구)에서 모든 노드를 한번씩 방문하며 거리를 누적하기에 적합합니다.
즉, 경로 추적 및 누적 값 계산이 용이하기 때문에 현재 문제에서는 DFS 접근이 옳다.
구현
이제 문제 이해를 마쳤으니, 알고리즘의 전체적인 흐름을 정의했다.
1. 입력값을 기반으로 1 ~ N 까지의 트리 구조에 노드 저장
2. 저장된 노드에 각 N-1 줄의 입력값(A,B,C)의 정보를 추가
a. A번 방에서 B번 방까지 거리 C, B번 방에서 A번 방까지 거리 C로 양방향 기록
3. DFS 기반으로 최장거리 찾기
문제는 DFS 기반으로 최장거리를 "한번에 찾기"를 어떻게 구현하는가 였다.
우리가 보편적으로 아는 방문 여부 체크 중심의 DFS 함수는 다음과 같다:
def dfs(node, visited):
visited[node] = True
for adj in graph[node]:
if not visited[adj]:
dfs(adj, visited)
그렇다면 어떻게 해야 여기에서 거리(distance)를 구할 수 있을까?
def dfs(node, dist, visited):
visited[node] = True
# dist: 현재까지 누적 거리 또는 비용
for adj, weight in graph[node]:
if not visited[adj]:
dfs(adj, dist + weight, visited)
다음과 같이 매개변수를 추가하고 누적 거리를 계산한다.
현재 문제에서는 1번 방으로 입구가 고정되어 있기 때문에 DFS를 1번만 진행하면서 모든 거리를 기록하고, 가장 큰 수(max)를 출력한다.
def dfs(node, dist, visited, distances):
visited[node] = True
distances[node] = dist
for adj, weight in tree[node]:
if not visited[adj]:
dfs(adj, dist + weight, visited, distances)
visited = [False] * (N + 1)
distances = [0] * (N + 1) # 1번 방부터 각 방까지의 거리 저장
dfs(1, 0, visited, distances)
print(max(distances))
개선점
접근 방법이나 핵심 포인트에 대한 이해는 맞게 했으나, 해설 및 코드를 읽고 내 코드가 가독성이나 효율성 모두 떨어진다는 생각이 들었다.
graph = [[] for _ in range(n + 1)]
visited = [False] * (n + 1)
dist = [0] * (n + 1)
def dfs(v):
visited[v] = True
for w, d in graph[v]:
if not visited[w]:
dist[w] = d + dist[v]
dfs(w)
dfs 함수 구현 시 매개변수를 줄이고, 접근하는 방식이 마땅히 떠오르지 않았는데, 생각보다 매우 단순했다.
for _ in range(1, n):
a, b, c = map(int, input().split())
graph[a].append([b, c])
graph[b].append([a, c])
입력 방식에서 이미 해당 노드에 대한 정보를 잘 포함하고 있기 때문에 기존의 dfs 함수 구조에서 큰 변화 없이 간단한 변경만으로도 수정이 가능하다는 것을 제대로 캐치하지 못한 것 같다. 문제를 잘 읽고 이해했다면, 위와 같은 접근이 가능하지 않았을까 해서 조금 아쉬웠다.
추가로, 평균적으로 해결하는 데 걸리는 시간이 45분인데, 그것보다 한참 시간이 더 걸렸다. (순수 구현에는 약 1시간 넘게 걸린 것 같다)
'개발자 일기 > 알고리즘 공부' 카테고리의 다른 글
| 작심큰일 챌린지 - Day 6. JadenCase 문자열 만들기 (미들러, Python) (1) | 2025.08.11 |
|---|---|
| 작심큰일 챌린지 - Day 5. 피보나치 비스무리한 수열 (미들러, Python) (5) | 2025.08.08 |
| 작심큰일 챌린지 - Day 3. 저울 (미들러, Python) (4) | 2025.08.06 |
| 작심큰일 챌린지 - Day 2. 안전 영역 (미들러, Python) (4) | 2025.08.05 |
| 작심큰일 챌린지 - Day 1. 소수 만들기 (미들러, Python) (4) | 2025.08.04 |




댓글